第一讲 引言

网络安全核心地位的关键目标

• 保密性（Confidentiality）
  • 数据保密性
  • 隐私性
• 完整性（Integrity）(包括不可否认性、真实性)
  • 数据完整性
  • 系统完整性
• 可用性（Availability）
• 真实性（Authenticity）
• 可追溯性（Accountability）

安全攻击

被动攻击

在未经用户同意和认可的情况下将信息或数据文件泄露给系统攻击者，但对数据信息不做任何修改

• 常见手段

  • 搭线监听

  • 无线截获

  • 其他截获
• 应对措施：重点在于预防

主动攻击

涉及某些数据流的篡改或虚假流的产生

• 分类
  • 阻断攻击
  • 伪造攻击
  • 重放攻击
  • 篡改攻击
  • 拒绝服务攻击
• 应对措施
  • 自动审计
  • 入侵检测
  • 完整性恢复

安全机制

安全机制要具备检测、防御或从安全攻击中恢复的能力，没有单一的机制能够提供所有的安全服务

• 特定的安全机制（specific security mechanisms）

  • 加密， 数字签名， 访问控制，数据完整性，认证交换，流量填充，路由控制，公证等
• 普遍的安全机制（pervasive security mechanisms）
  • 可信功能，安全标签，事件检测，安全审计跟踪，安全恢复

安全服务

• 可认证性 Authentication
• 访问控制 Access Control
• 机密性 Confidentiality
• 完整性 Integrity
• 不可否认性 Non-repudiation
• 可用性 Availability

第二讲 传统加密技术

密码学

• 密码编码学
  • 研究内容：主要研究对信息进行编码，实现对信息的隐蔽
  • 特征
  • 密码编码学常用运算：代替与置换
  • 所用的密钥数：单钥与双钥
  • 处理明文的方法：分组密码与流密码
• 密码分析学
  • 研究内容：主要研究如何破解密文的方法
  • 攻击的两种常用方法
  • 密码分析学： cryptanalytic attack
  • 穷举攻击： brute-force attack

保护密码算法还是密钥

1. 与维护算法的保密性相比，维护密钥的保密性更容易。

2. 万一密钥暴露了，Alice 和 Bob 可以很容易地更换密钥；而万一算法被攻破，重新设计一个很好的加密算法要难得多。

3. 万一有多对人员需要加密其通信，这些人可以使用相同的算法和不同的密钥，而使用不同的程序则太难。

加密算法

• 凯撒密码：共有密钥25个、移位、替换
• 单表代替密码：任意地打乱字母的顺序，密钥数目： 26！＞ 4 × 10^{26}
• playfair 密码：多字母代替密码，密钥空间：25！≈1.6×10^{25}
• Hill 密码
  • 加密：C≡KP mod 26，其中，K为密钥矩阵，P、C分别为明、密文分组
  • 解密：P≡K^{-1}C mod 26
• 维吉尼亚密码
• 置换密码

第三讲 分组密码与 DES

Feistel 密码结构

混淆和扩散

• 混淆：使得密文的统计特性与密钥的取值之间的关系尽量复杂

• 扩散：明文的统计特征消散在密文中，使得明文和密文之间的统计关系尽量复杂

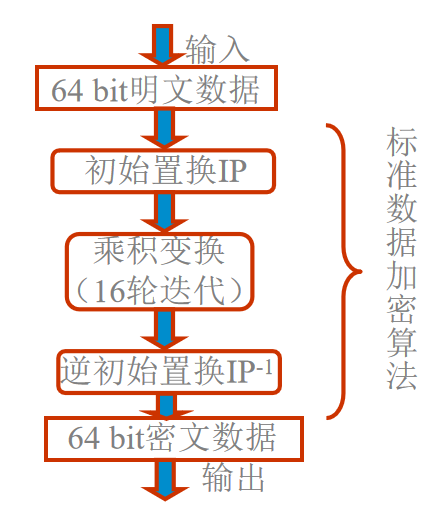
DES 加解密

1. 两次置换（初始置换和初始逆置换）

2. 密钥控制下的十六轮迭代加密

3. 轮密钥生成

4. DES 是一种用 56 位密钥来加密 64 位数据的方法

雪崩效应

明文或者密钥的某一位发生变化，会导致密文很多位的变化

第四讲 代数基础

模运算性质

• 对称

• 传递

  计算2^{64} mod 2012

\begin{flalign*} &2^2 =4 mod 2012\\ &2^4 =16 mod 2012\\ &2^8 =256 mod 2012\\ &2^{16}=65536 ≡1152 mod 2012\\ &2^{32}=1152^2 ≡1196 mod 2012\\ &2^{64}=1196^2 ≡1896 mod 2012& \end{flalign*}

欧几里得算法（辗转相除法）

求gcd(1970, 1066)

\begin{flalign*} &令a=1970，b=1066\\ &1970=1×1066+904\\ &1066=1×904+162\\ &904=5×162+94 \\ &…… …… \\ &10=1×6+4\\ &6=1×4+2\\ &4=2×2\\ &因此gcd(1970, 1066)=2 & \end{flalign*}

求乘法逆元

已知28与81互素，求81 mod 28的逆元。

\begin{flalign*} &81=2×28+25\\ &28=1×25+3\\ &25=8×3+1\\ \\ &1=25-8×3\\ & =25-8×(28-25)\\ & =(-8)×28+9×(81-2×28)\\ & =9×81+(-26)×28\\ &所以81×9≡1 mod 28，同时 28×（－26）≡1 mod 81, 81 mod 28的逆元为9\\ &而28 mod 81的逆元为－26≡55& \end{flalign*}

群环域基本概念

• 群：群是定义了一个二元运算“•”的集合G，表示为(G，•)$，并且满足以下公理：
  • 封闭性
  • 结合律
  • 单位元
  • 逆元
• 环：设R是至少含有两个元素的集合，R中定义了两种运算“+”和“•”，如果代数系统<R,+, • >满足以下公理，则称其为环
  • R关于加法构成交换群
  • R关于乘法构成半群，即乘法满足封闭性和结合律
  • 分配律
• 域：设F是至少含有两个元素的集合，F中定义了两种运算“+”和“•”，如果代数系统<F,+, • >满足以下公理，则称其为域
  • F是一个整环
  • 有乘法逆元：对于任意a ∈F，存在a-1∈F，使得a • a -1=a-1 • a=1成立

基于多项式的有限域构造及运算

密码学中为什么用 GF(2^m)

第五讲 AES 加密

AES 加解密过程

• 字节代替
• 行移位
• 列混合
• 轮密钥加

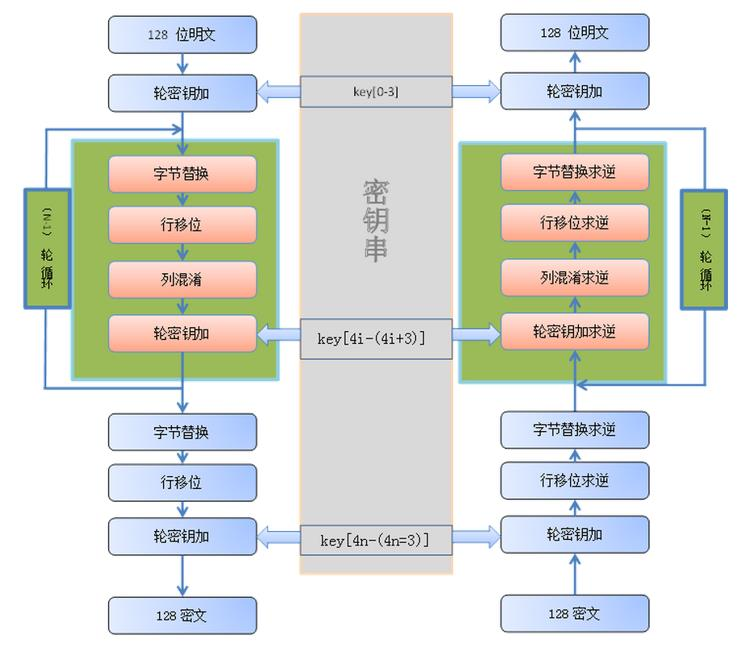
• 轮函数四步：字节代替、行移位、列混合、轮密钥加（注：最后一轮无列混合）

AES 密钥生成过程

第六讲A 分组密码工作模式

2DES

• 加密：C = EK2(EK1(P))
• 解密：P = DK1(DK2(P))

双重 DES 为什么不行？（中间相遇攻击）

中间相遇攻击是一种针对双重加密算法的攻击，需要一个已知的明、密文对，本质上，明文在双重加密中被加密产生中间值，密文在双重加密中被解密产生中间值，表查找方式可以用这种方法改进对密钥的蛮力尝试。

• 已知明文攻击可以成功对付密钥长度为 112 位的 2DES
  • C = E_{K2}(E_{K1}(P)), X = E_{K1}(P) = D_{K2}(C)
  • 用所有可能的密钥加密明文并存储
  • 用所有可能的密钥解密密文，并与存储的X匹配。如果有相等的，那么获得一组可能的密钥对，并用新的明密文对验证。
  • 概率分析：2^{112}/2^{64}=2^{48}，2^{48}/2^{64}=2^{-16}，两组明密文对后，正确密钥的概率是1-2^{-16}；三组明密对后，正确密钥的概率是1-2^{-80}
  • 付出数量级为 O(256),比攻击单DES的O(255)多不了多

为什么需要分组密码工作模式

如果待加密的消息过长，需要将消息分组后，一组一组的使用加密算法，然后输出密文。在这一过程存在两个问题：

• 分组密码不能隐蔽数据模式，即相同的明文分组对应着相同的密文分组，容易受到攻击
• 分组加密不能抵抗重放、插入和删除攻击等。把分组密码算法用在不同环境时，环境不同要求也不同。

为了满足不同要求，需要通过改变分组密码输入和输出的形式，得到分组密码的不同工作模式。

五种工作模式的具体构造及特点

模式	特点	典型应用
电码本 ECB	用相同的密钥分别对明文组加密	单个数据的安全传输
密文分组链接 CBC 有 IV	加密算法的输入是上一个密文组合下一个明文组的异或	加密长度大于 64 位明文 P、认证
密文反馈 CFB 有 IV	分组任意，安全性优于 ECB 模式加、解密都使用加密运算（不用解密运算）	加密长度大于 64 位的明文，分组随意；可作为流密码使用、认证
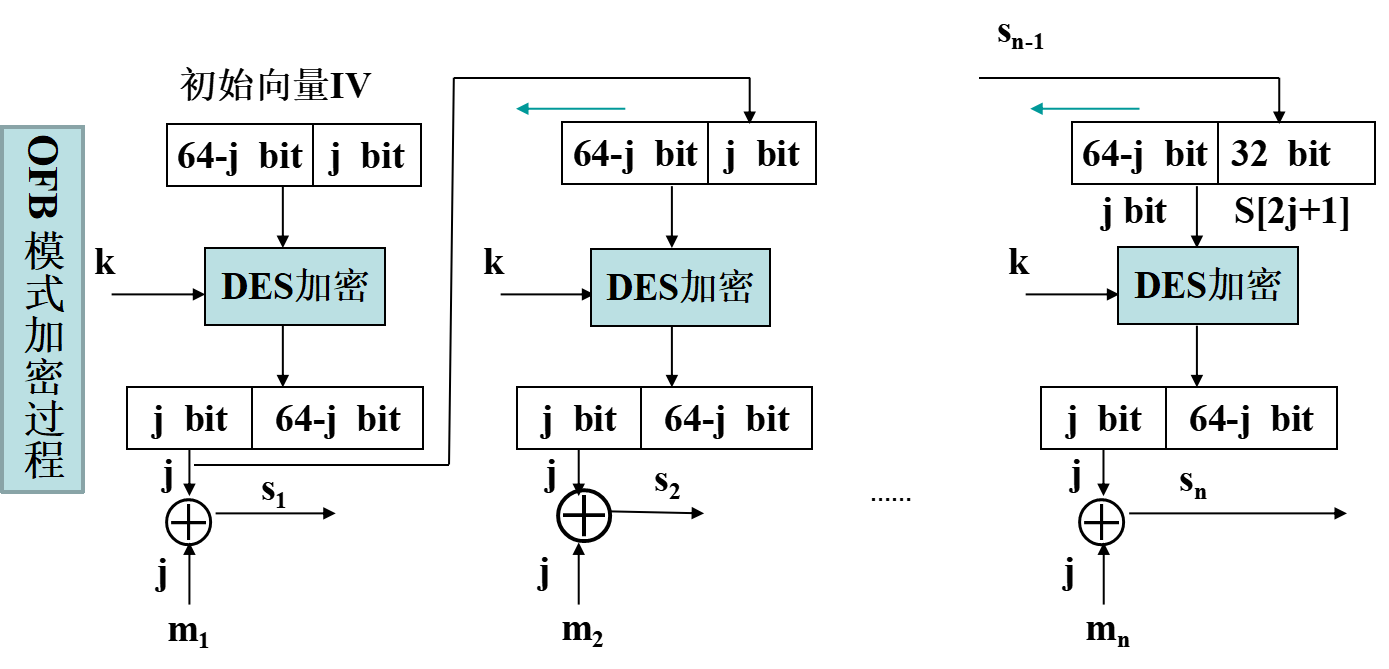
输出反馈 OFB 有 IV	抗消息流篡改攻击的能力不如 CFB	噪声信道上的数据流的传输,比如卫星通信
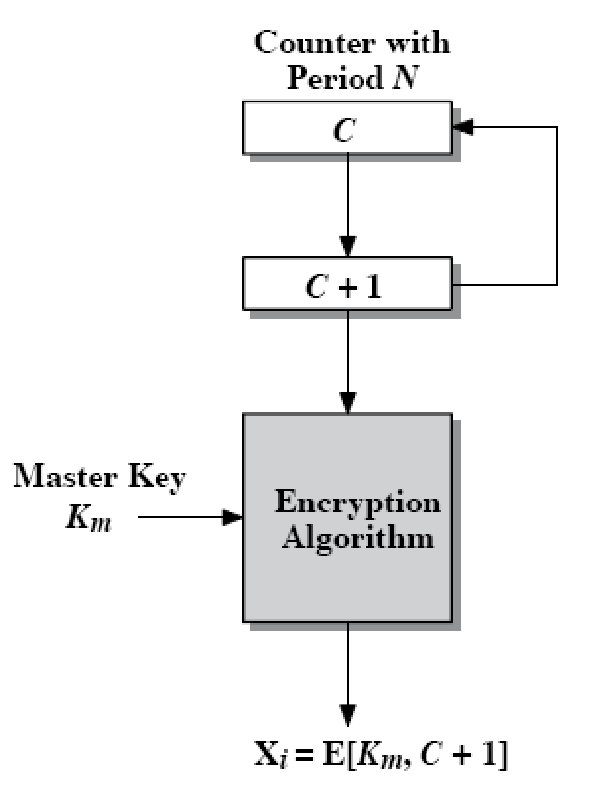
计数器 CTR 有 IV	硬(软)件效率：并行、预处理、随机访问、可证明的安全性、简单性：只用到加密算法	分组传输，高速需求的应用

第六讲B 随机数与流密码

随机数基本概念

• （随机数在密码学中的）应用
  • 临时交互号，用于防止重复攻击
  • 会话密钥产生
  • RSA算法中密钥的产生
• （对随机数产生的）要求
  • 随机性和不可预测性

基于密码学的随机数生成

• 循环加密：设E为加密算法，C为计数器，预置其初值为0，K_m为保密的主密钥，每加密一次，产生一个随机数，同时计数器的值加1

  

• 用DES的输出反馈方式产生

  

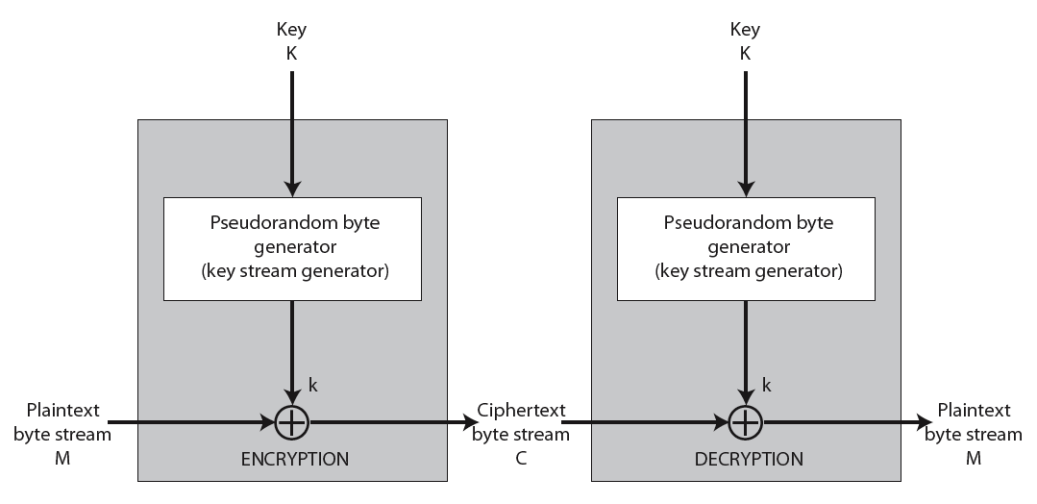
流密码的基本原理

• 消息的处理以字节为单位以流的方式进行
• 伪随机密钥流 keystream
• 密钥流与明文进行按位的异或运算 (XOR)
• 密钥的随机性破坏明文中的统计规律 C_i = M_i \ \ XOR \ \ StreamKey_i
• 不能重复使用密钥流，否则将被破译

第七讲 数论基础

素数基本概念

费马小定理、欧拉定理、素性检测概率算法

离散对数的基本概念

第八讲 公钥密码学与RSA

对称密码弱点

1. 密钥量大
2. 密钥管理困难：传递、换发、保存
3. 无法实现网络中的数字签名、消息认证、用户认证等应用

系统中有 n 个用户，两两进行保密通信：

每个用户需要有 n-1 个密钥 总密钥数C(n,2) = n(n-1)/2

Shamir 盒及公钥密码基本原理

Shamir 盒模型的两点启示：

• 不事先交换密钥就能进行秘密通信
• 加密、解密的密钥可以分开

公钥密码基本原理：

• 使用两个不同的密钥，一个用于加密，一个用于解密

• 用于加密的密钥 E_k 可以公开，用于解密的密钥D_k 保密

• E_k 与 D_k 之间有联系，但不能由 E_k很容易地算出 D_k

RSA 公钥密码基本原理及计算

• RSA算法密钥的建立

  • 选择素数：p = 17 \& q = 11，计算n = p q =17 x 11 = 187

  • 计算 ø(n) = (p–1)(q-1) = 16 * 10 = 160

  • 选择 e: gcd(e, 160) = 1; 选择 e = 7

  • 确定 d: d*e = 1 mod 160 且 d < 160 d = 23 因为 23 *7=161= 10 * 160+1

  • 公钥 PU = { 7, 187 }，私钥 PR = { 23, 187 }
• 明文消息：m = 88 (<187)
• 加密：c = 887 mod 187 ≡ 11
• 解密：m = 1123 mod 187 ≡ 88

第九讲 其他公钥密码体制

(重点)Diffie-Hellman 密钥交换

中间人攻击

1. Darth生成两个随机数X_{D1}和X_{D2}，随后计算相应的公钥Y_{D1}和Y_{D2};

2. Alice将Y_A传递给Bob;

3. Darth截获了Y_A，将Y_{D1}传给Bob，同时计算

   K_{2}=\left(Y_{A}\right)^{X_{D 2}} \bmod q

4. Bob收到Y_{D1}，计算

   K_{1}=\left(Y_{D1}\right)^{X_{B}} \bmod q

5. Bob将Y_B传给Alice;

6. Darth截获了Y_B，将Y_{D2}传给Alice，Darth计算

   K_{1}=\left(Y_{B}\right)^{X_{D1}} \bmod q

7. Alice收到Y_{D2}，计算

   K_{2}=\left(Y_{D2}\right)^{X_{A}} \bmod q

ElGamal 密码体制

• 困难问题：离散对数问题

• 特点：加密是概率算法—有随机数参与

• 加密过程

  • 设m为明文，随机选择整数k，k与p-1互素，计算
  • c_1 ≡ g^k mod p
  • c_2 ≡ my^k mod p
  • 密文c=(c1, c2)

• 解密过程

  • 收到密文c=(c1, c2)后，接收方进行如下计算 \begin{array}{l} c_{2} \cdot\left(c_{1}^{x}\right)^{-1}=m y^{k} \cdot\left(g^{k x}\right)^{-1} =m g^{k x}\left(g^{k x}\right)^{-1} \equiv m \bmod p \end{array}

第十讲 密码学Hash函数

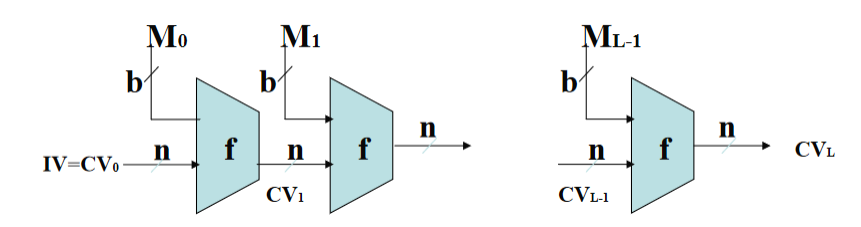
Hash 函数的基本特性、基本设计框架

任意长度的明文进行变换得到相应的函数值，称为散列值(长度固定)。

• 用途：消息认证码、数字签名预处理、从口令衍生密钥等。

• 特性：

  • 对任意长度输入进行变换，得到固定长度输出
  • 求逆不可行 抗原像攻击/单向性
  • 对给定 x，很难找到x’≠x，使得h(x’)=h(x) 抗弱碰撞性
  • 很难找到一对不同的x, x’，使得 h(x’)=h(x) 抗强碰撞性

  满足1-2为单向散列函数，1-3为弱散列函数，1-4 为强散列函数

  

  CVL 为最终的哈希输出

生日攻击基本原理

1. 攻击者产生一份合法的明文，再产生232个不同的明文变形，构成一个合法明文组；
2. 生成一份非法明文，构造232个不同的非法明文变形，产生一个非法明文组；
3. 分别对以上两个组产生散列值，在两组明文中找出具有相同散列值的一对明文。如果没有找到，则再增加每组明文变形的数目，直至找到。由 “生日悖论”可知，其成功的概率很大；
4. 于是，攻击者找到了一则与合法明文（至少内容合法）具有相同散列值的非法明文。

第十一讲 消息认证码

消息认证码如何设计？基于hash和基于密码的(大致思路)

基于密码 hash 函数的 MAC**：**HMAC

• 不用分组密码，而用 hash 函数来产生 MAC，因为 hash 函数一般都较快 没有出口限制，(分组密码有出口限制)
• hash 函数不依赖于密钥，所以不能直接用于 MAC
• 建议: KeyedHash = Hash( Key || Message )

基于密码的：采用分组密码（DES）的链接工作（CBC 模式）模式，并把最后分组作为 MAC

看复习PPT，最好能直接画出框图

CMAC：基于密码的消息认证码，框架与 DAA 类似，加密用 AES 和 3DES 实现

第十二讲 数字签名

数字签名的基本特性和用途，如何构造 （私钥签名，公钥验证）

• 特性：
  1. 签名值必须依赖于所签的消息
  2. 必须使用对于发送者唯一的信息，以防止伪造和否认
  3. 产生签名比较容易
  4. 识别和验证签名比较容易
  5. 伪造数字签名在计算上是不可行的。包括已知数字签名，伪造新的消息和已知消息，伪造数字签名
  6. 保存数字签名的拷贝是可行的

第十三讲 密钥管理与分发

典型的基于对称加密的密钥分发方案（步骤）

公钥基础设施

1. 公钥基础设施 (PKI) 系统是有硬件、软件、人、策略和程序构成的一整套体系

2. 公钥基础设施实体：

   • 端实体
   • 签证机构 CA

   • 注册机构 RA

   • 证书撤销列表发布 CRL
   • 证书存储库

公钥分发机制、X.509 证书、PKI 基本概念

第十四讲 用户认证

Needham-Schroeder 认证协议、Kerberos 基本原理及步骤、基于公钥的远程认证步骤

第十五讲 传输层安全

SSL 协议设计思路、SSL 握手协议过程以及其能对抗攻击的原因

SSL握手协议的具体交互过程

1. 建立安全协商：交换 Hello 消息，对于算法、交换随机值等协商一致
2. 服务器鉴别：交换必要的密码参数，以便双方得到统一的 premaster secret

3. 客户端鉴别和密钥交换：交换证书和相应的密码信息，以便进行身份认证产生 master secret

4. 结束：把安全参数提供给 SSL 记录层检验双方是否已经获得同样的安全参数

SSL的安全性

• 保护主密钥
• 保护服务器的私钥
• 使用良好的随机数
• 证书链检查
• 算法选择（强度）

第十六讲 IP安全

IPSec 基本原理、AH、ESP、传输模式、隧道模式、密钥管理基本思路

IPsec 优点

1. 对应用和最终用户透明

2. 在防火墙或路由器中实现时可以防止 IP 旁路

3. 需要时 IPSec 可以提供个人安全性

4. 弥补 IPv4 在协议设计时缺乏安全性考虑的不足

IPsec 两种模式：传输模式和隧道模式

• 传输模式为上层协议提供保护，用于两台主机间的端到端通信

• 隧道模式对整个 IP 数据包提供保护